The domain of a function is defined as the set of all possible values that the independent variable usually ‘x’ can take so that the function is real. Domain also presents exceptionally crucial information concerning the range and behavior of the function especially graphically for functions that involve square roots. In this article, let us get to know more about the domain of square root functions and how to interpret the graphs and the functions accurately.
Analysis of the Definition of the Square Root Function
The square root function is one of the most fundamental mathematical functions and is represented as:
f(x) = √x
This function is defined only in case the expression under the radical sign, or the argument of the radical, commonly referred to as the radicand, is non-negative or greater than or equal to zero. For example:
If x = 4, then f(x) = √4 = 2.
If x = -4, there is no real number which, when squared is equal to -4 Thus, the square root is not real in the real number system.
Domain and Range of Square Root of Functions
The square root of a negative number is not a real number. In other words the square root function can only take in non-negative numbers.
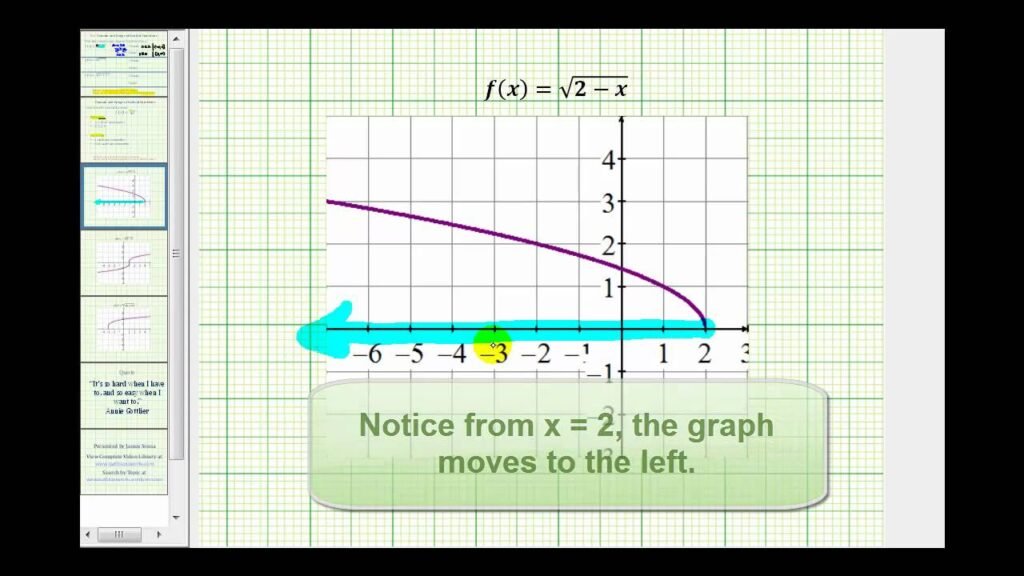
To further explain the domain of the square root function f(x) = √x, it shall refer to all non-negative constant ‘x’. This means that the domain of the square root function is from 0 up to the positive infinity, (0, ∞). It also has 0 in its domain as you will quickly confirm from the following lessons:
It should be noted that usual sign of the square root is a plus namely √25=5 or -5 with the condition that 5²=25 and (-5)²=25. The domain of the square root function (above, I talked only about its x-values) actually does not contain negative numbers as a range because if it did, then it does not pass the vertical line test, and, in the case where an input gives two outputs, it isn’t a function.
We also observe that the range of the square root function f(x) = √x is [0, ∞) which is indeed it’s domain. That is why it also ranges from 0 in this case.
Square Root Graph
You know the general appearances of the square root curves from what we have earlier seen. But now let us turn to the next example to find out how to draw y = sqrt(x). From the above work we noted that the domain and the range of the parent square root function f(x) = √x is the set of all nonnegative rea numbers. Therefore the graph of square root function f(x) = √x exists only in the first quadrant of a coordinate axis.
This implies that we can obtain its graph by plotting a table of values which involves some arbitrary values of elements of domain of x belonging to the interval [0, ∞) which are then substituted into y = √x to obtain corresponding values of y. Then we can get determined some points that are to be placed on xy plane, and join all these points by curve.
| x | y |
| 0 | √0 = 0 |
| 1 | √1 = 1 |
| 4 | √4 = 2 |
Graphing of Any Square Root Function
Now we saw how to graph the parent square root function f(x) = √x. Below are the procedure that is helpful in graphing any square root function of the type f(x) = a√ (b(x – h)) + k in general.
Step 1: Find the domain of the function asking “the expression inside the square root” to be greater than or equal to 0 using the solution on x.
Step 2: A square root function always has a domain of x in the interval [h,∞) The range of any square root function is also y ≤ k where ‘k’ represents the vertical shift of the whole function f(x) = a√(b(x – h)) + k.
Step 3: Make a table of values in which ‘x’ is the independent variable and ‘y’ is the dependent variable, choose some random numbers for ‘x’ ranging from the first value of the domain and substitute in the given function and get the value of ‘y’.
Step 4: Place all the points on the plane and draw a curve through all the points as well as outside them with using similar direction.
Properties of Square Root Function
Below are the highlights/properties that are to be remember about the square root function f(x) = √x .
- Its domain is [0, ∞).
- Its range is [0, ∞).
- It has no relative maxima but it has minimum at (0, 0)
- There are no asymptotes founded in a square root function.
- We can notice that the function is increase through out its domain that is [0, ∞).
- The function f(x) = √x has the derivative of the first degree at the point (0, 0) and there are no second degree points of inflection.
Conclusion
One should note that the range of values with respect to which the square root function is defined is limited to the interval [0; ∞). This limitation retains the essence of the function as a real one because the square root of negative number cannot be found in real numbers.
As with the domain of the square root function, the range of the square root function is also non negative, that is from 0 to positive infinity. As a picture the square root function is represented by a curve that is contained only in the first quadrant of the coordinate plane and commence at the origin.




